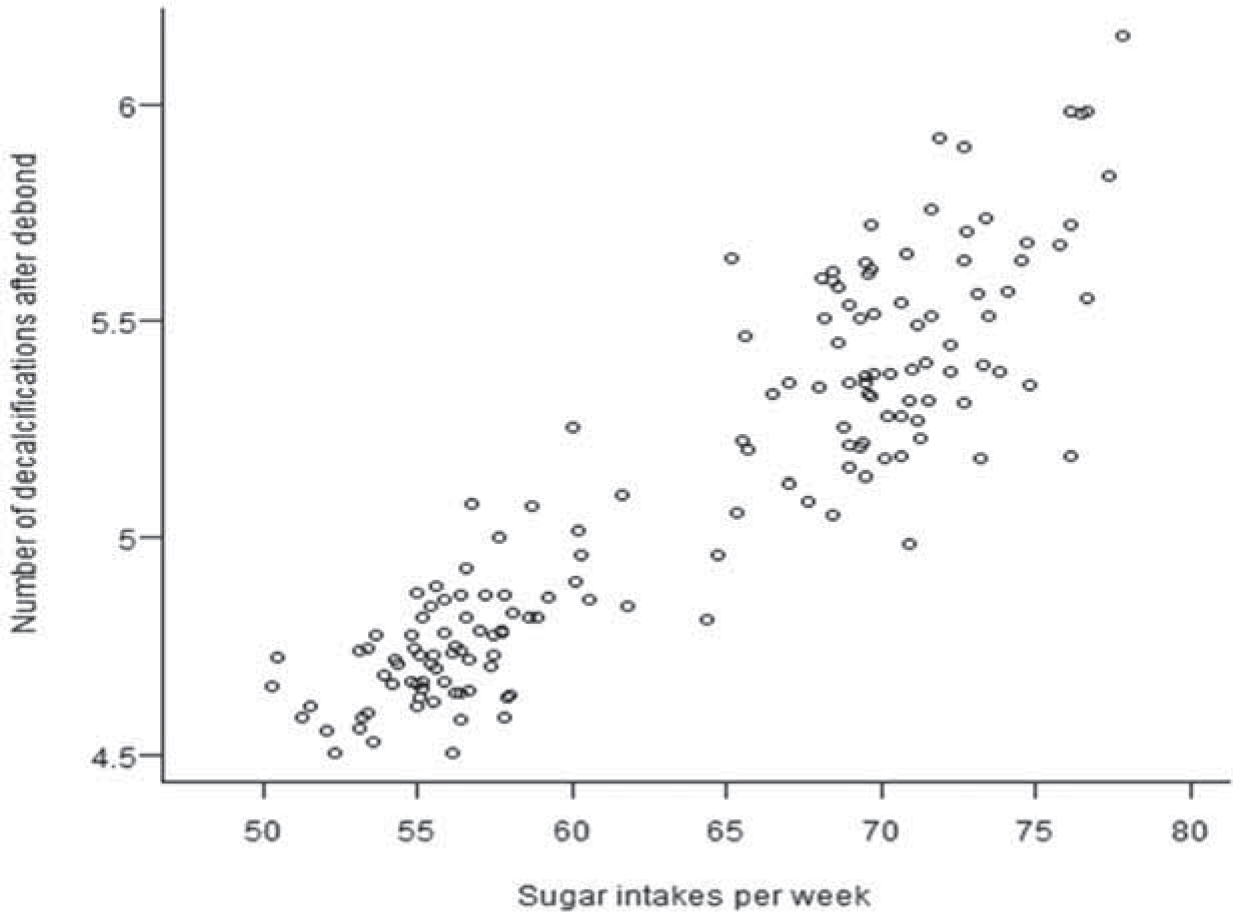
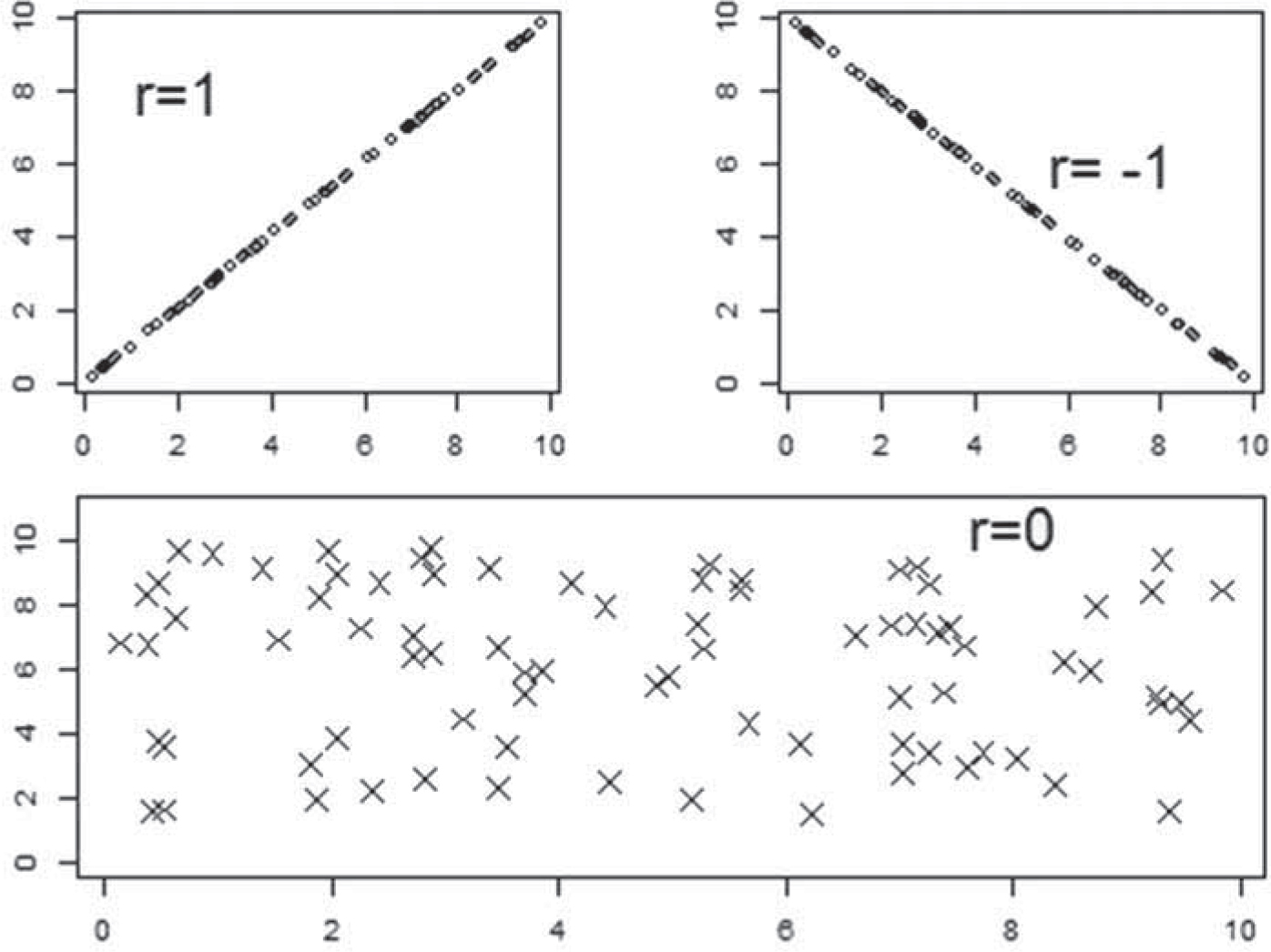
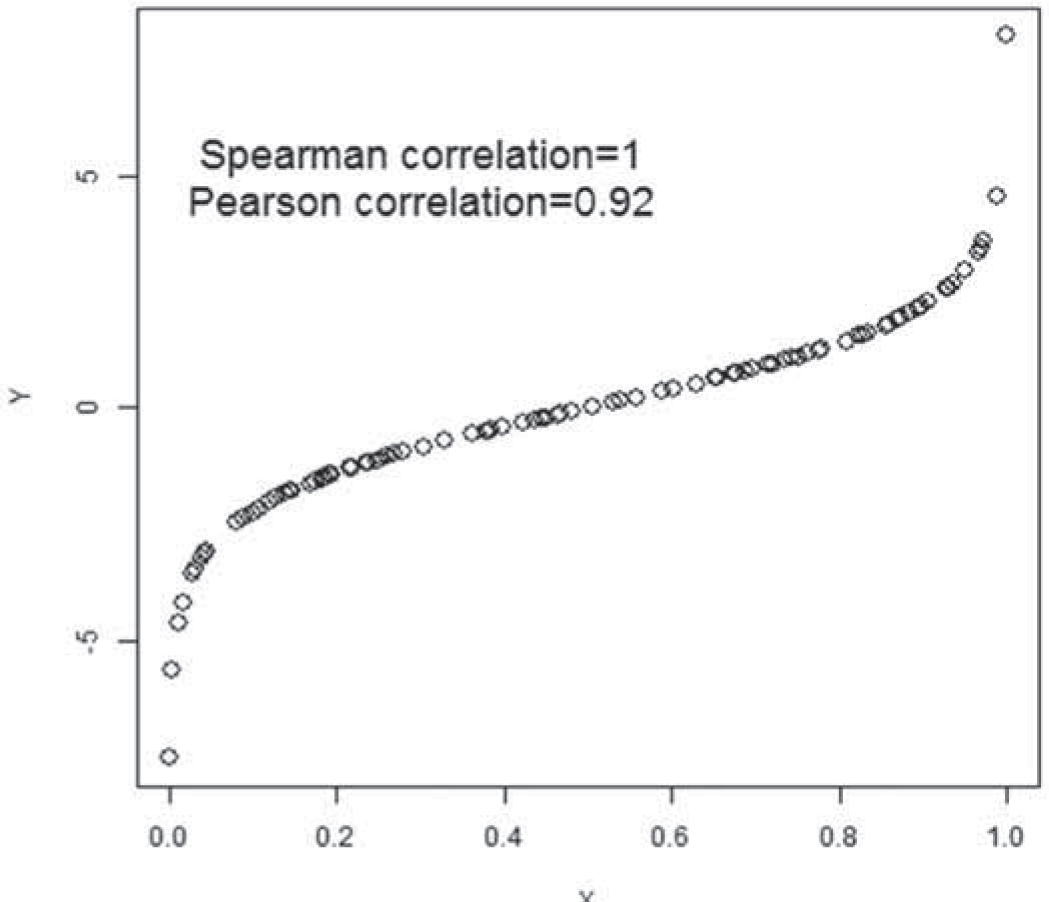
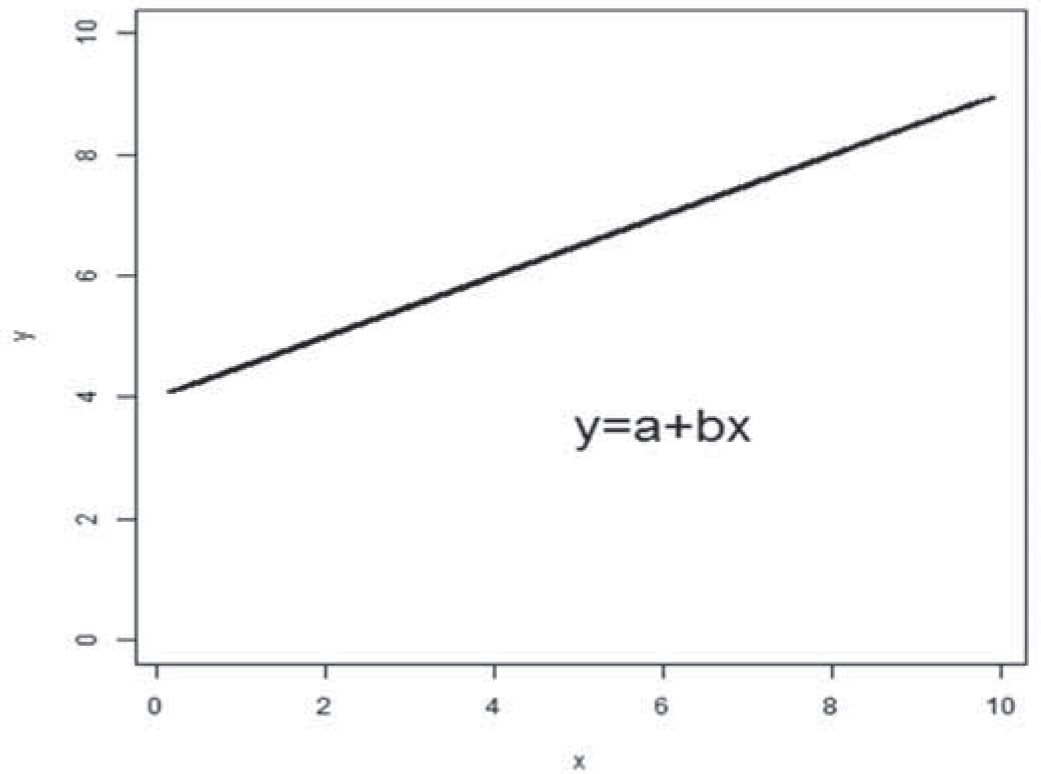
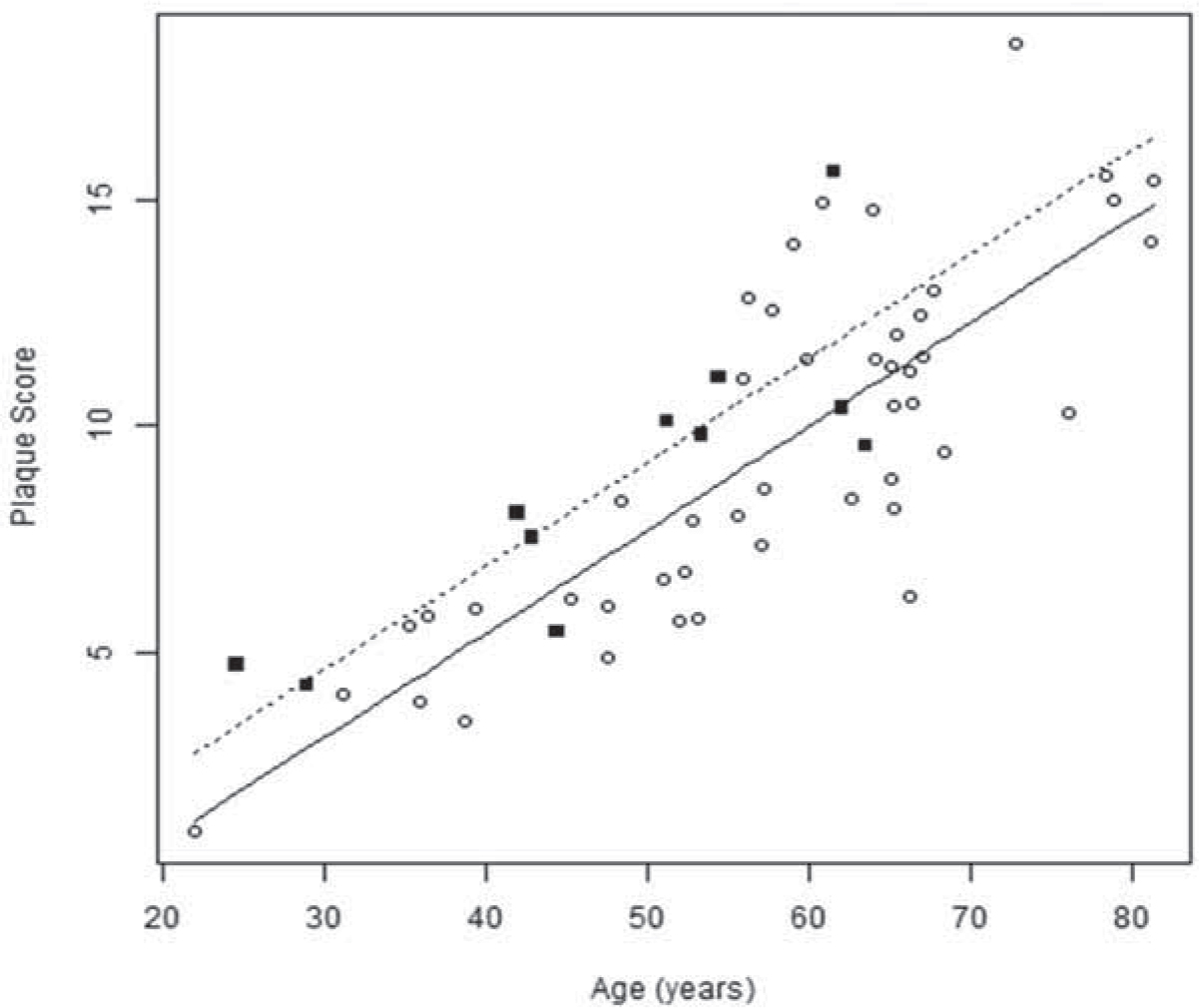
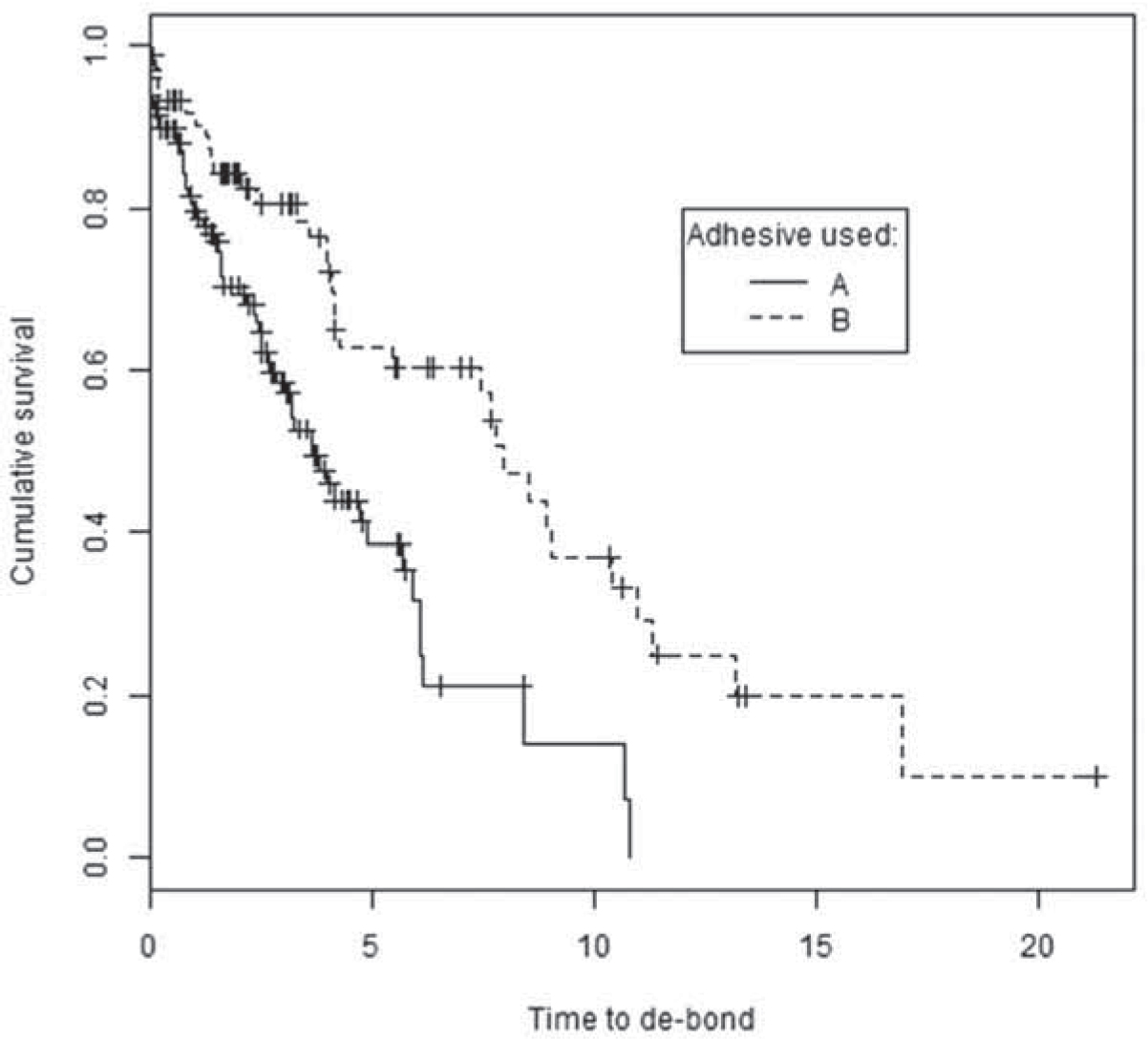
Abstract
There is an increasing volume of research undertaken within orthodontics and with this comes a need to evaluate what is available. This short series aims to help the orthodontist revise basic concepts of critical appraisal and pertinent statistics.